Opportunity
Why backtesting is no fairy godmother and how it can backfire on you by telling a story only to be dreamt of.
Statistics and machine learning are powerful tools to analyze financial data. Both academic and finance communities widely recognize that their overzealous application to the same data sources, time and again, is not the right approach.
Practitioners in quantitative finance often rely on Sharpe Ratio, Student-t test and an entire line-up of related statistics to evaluate the results of their backtesting. Although being valuable tools to understand whether the results are a statistical fluke, they do not tell you anything about the potential for false discovery1 2.
A backtesting is nothing else than a static snapshot of what could best have been done in the past. Nonetheless the opportunity to exploit, only lies in the future, so you will have to assume the future more or less matches the past. Backtesting requires a far from negligible number of choices, based on data or fixed arbitrarily ab initio, like parameters, selection of trading strategies, investment universe, etc. The numerous degrees of freedom involved in these choices often end up in an overfit of the data.
Methodologies exist to mitigate the risks of overfitting. To name a few, relying only on the conclusions of published and well replicated academic papers, saving an out-of-sample dataset to confirm results, using a rolling window to calibrate parameters, taming statistics to account for multiple hypothesis testing or applying cross-validation. But all have their drawbacks and often force you, explicitely or implicitely, to make additional choices.
For example, by relying on previous studies, you simply accept that numerous researchers looked at the same data over and again, possibly not independently as they implicitly relied on results from previous research as the starting point to theirs. The odds that significant features were found by chance are material given the data mining involved.
Another typical approach is to rely on a rolling window to sample the data, then calibrate a model on it and later use extra out-of-sample data to select the final models. Those will be used for a time and the process will start again for a shifted time window. You are probably familiar with how final results depend on the choices made and how notoriously difficult it is to handle the process. Inter alia you have to choose the:
- set of models to be calibrated,
- sizes of the in-sample and out-of-sample periods,
- time period in which you will actually trade the models before recalibrating the whole.
At this point you realise there exists a wide range of possible parameters with near optimal performance which brings forward two observations. First, the results chosen for presentation are almost always based on the optimal set of parameters. Only subsequently is reference made to results not depending much on those chosen parameters. Second, you still need to acknowledge that in contrast to the reality which will be faced, data had first to be observed before optimal parameters could be inferred!
The final step is to recognize that the performance you observe as a result of backtesting is probably the best you could have achieved in the past, had you known the future in advance. This sounds evident, yet is of the utmost importance. Ask yourself: had I started trading on the very first day of my dataset, how would I have acted? The human solution to this conundrum is straightforward: apply trial and error adjusting your opinion as experience from new evidence accumulates. A typical Bayesian approach.3
Oxford English Dictionary defines Intelligence as “The ability to acquire and apply knowledge and skills.” What if we could build an Artificial Intelligence which would replicate human learning principles and offer to apply them systematically without biases nor limitations? Such thoughts and questioning paved the way to AGNOSTIC’s development.
The future has many names:For the weak, it means the unattainable.For the fearful, it means the unknown.For the courageous, it means opportunity.Victor Hugo
Multiple hypothesis testing, i.e. the repetition of a single hypothesis test time and again, matters. In general, if we perform m independent hypothesis tests, what is the probability of at least one false positive?
\(P(\textrm{ Making an error }) = \alpha\)
\(P(\textrm{ Not making an error }) = 1 - \alpha\)
\(P(\textrm{ Not making an error in m independent tests }) = (1 - \alpha)^m\)
\(P(\textrm{ Making at least 1 error in m tests }) = 1 - (1 - \alpha)^m\)
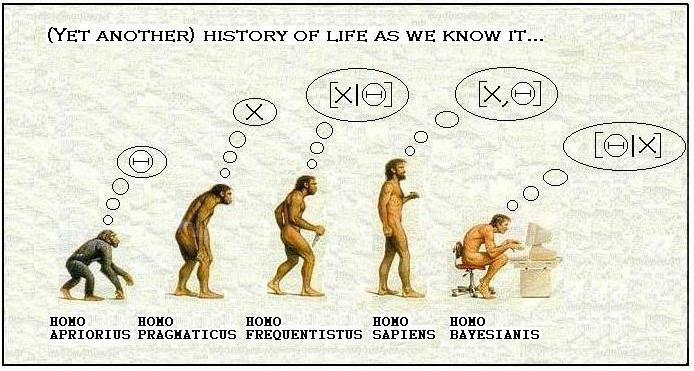
For example, for 50 tests using the same data, the probability of making at least one false positive using 5% confidence is \(P=1-(1-0.05)^{50}=92.3\%\), hence very probable.↩︎- A natural evolution of man towards bayesian statistics. “\(|\)” stands for “conditional to”, \(\Theta\) stands for hypothesis and \(X\) for evidence (i.e. data collected). Frequentists evaluate the probability of the data collected given an hypothesis they made. Bayesians evaluate the probability of the hypothesis given the data collected.
↩︎